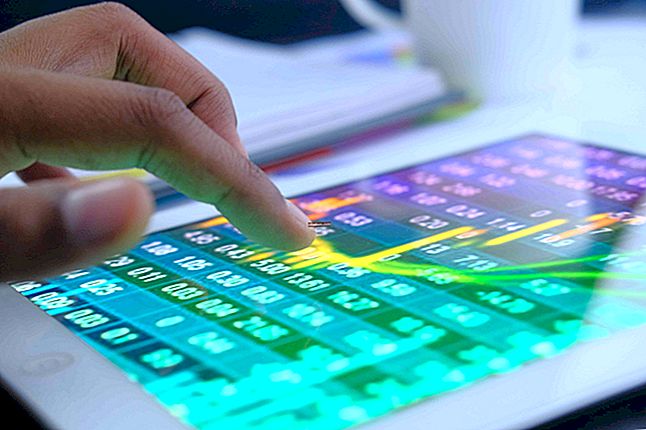
Ang pormula para sa kasalukuyang halaga ng isang annuity na dapat bayaran
Ang kasalukuyang halaga ng isang may bayad sa annuity ay ginagamit upang makuha ang kasalukuyang halaga ng isang serye ng mga pagbabayad na cash na inaasahang gagawin sa mga paunang natukoy na hinaharap na mga petsa at sa mga paunang natukoy na halaga. Ang pagkalkula ay karaniwang ginagawa upang magpasya kung dapat kang kumuha ng isang lump sum payment ngayon, o sa halip ay makatanggap ng isang serye ng mga pagbabayad ng cash sa hinaharap (tulad ng maalok kung manalo ka ng isang loterya).
Ang pagkalkula ng kasalukuyang halaga ay ginawa gamit ang isang rate ng diskwento, na halos katumbas ng kasalukuyang rate ng pagbalik sa isang pamumuhunan. Kung mas mataas ang rate ng diskwento, mas mababa ang kasalukuyang halaga ng isang annuity. Sa kabaligtaran, ang isang mababang rate ng diskwento ay katumbas ng isang mas mataas na kasalukuyang halaga para sa isang annuity.
Ang pormula para sa pagkalkula ng kasalukuyang halaga ng isang annuity na dapat bayaran (kung saan nagaganap ang mga pagbabayad sa simula ng isang panahon) ay:
P = (PMT [(1 - (1 / (1 + r) n)) / r]) x (1 + r)
Kung saan:
P = Ang kasalukuyang halaga ng annuity stream na babayaran sa hinaharap
PMT = Ang halaga ng bawat pagbabayad sa annuity
r = Ang rate ng interes
n = Ang bilang ng mga panahon kung saan binabayaran
Ito ang kapareho ng pormula para sa kasalukuyang halaga ng isang ordinaryong annuity (kung saan nagaganap ang mga pagbabayad sa magtapos ng isang panahon), maliban sa kanang bahagi ng pormula ay nagdaragdag ng dagdag na bayad; ang account na ito para sa katotohanan na ang bawat pagbabayad ay mahalagang nangyayari sa isang panahon nang mas maaga kaysa sa ilalim ng ordinaryong modelo ng annuity.
Halimbawa, ang ABC International ay nagbabayad ng isang third party ng $ 100,000 sa simula ng bawat taon para sa susunod na walong taon kapalit ng mga karapatan sa isang pangunahing patent. Ano ang gastos sa ABC kung babayaran nito kaagad ang buong halaga, sa pag-aakalang isang rate ng interes na 5%? Ang pagkalkula ay:
P = ($ 100,000 [(1 - (1 / (1 + .05) 8)) / .05]) x (1 + .05)
P = $ 678,637
Ang kadahilanan na ginamit para sa kasalukuyang halaga ng isang annuity dahil ay maaaring makuha mula sa isang pamantayan ng talahanayan ng kasalukuyang mga kadahilanan ng halaga na inilalagay ang mga naaangkop na mga kadahilanan sa isang matrix ayon sa tagal ng panahon at rate ng interes. Para sa isang mas mataas na antas ng katumpakan, maaari mong gamitin ang naunang pormula sa loob ng isang elektronikong spreadsheet.